* 66번~70번
66. 다음 중 2차계에서 overshoot를 가장 크게 하는 제동비(damping factor; ζ)는?
① 0.1
② 0.5
③ 1
④ 10
정답 : 1번
----------------------------------------------------------------------------------------------------
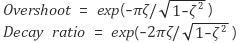
이런 식도 있긴한데, 식으로 봐도 되고,
ζ>1이면 과도감쇠, ζ=1이면 임계감쇠 (두 경우 overshoot 없음)
ζ<1이면 과소감쇠 인 점을 생각해서 가장 작은 값을 고르면 될듯하다.
----------------------------------------------------------------------------------------------------
67. 개방회로 전달함수가 $\frac{K_{c}}{(s+1)^{3}}$인 제어계에서 이득여유(gain margin)가 2.0이 되는 ${K}_{c}$는?
① 2
② 4
③ 6
④ 8
정답 : 2번
----------------------------------------------------------------------------------------------------
16년 4회 51번과 식만 조금 다르고 같은 문제이다.
https://for-freeedom.tistory.com/141
화공기사 2016년 4회 기출 풀이(*51번,52번,*53번,54번,*55번)
* 합격을 위해 맞춰야할 문제 : 52번, 54번 51. 안정도 판정에 사용되는 열린루프 전달함수가 인 제어계에서 이득여유가 2.0 이면 K 값은 얼마인가? ① 1.0 ② 2.0 ③ 5.0 ④ 10.0 정답 : 1번 ----------
for-freeedom.tistory.com
이득여유(gain margin) = $ \frac{1}{A R_{O L}\left(\omega_{c o}\right)} $
$A R_{O L}\left(\omega_{c o}\right)$ : $\omega=\omega_{c o}$ 일 때(위상각이 -180˚) 개회로 전달함수의 진폭비
(AR : 진폭비, $\omega_{c o}$ : 크로스오버 주파수)
$A R_{O L}\left(\omega_{c o}\right) = 0.5$
주어진 개루프 전달함수의 위상각과 진폭비를 계산하기 위해,
s = jw 를 대입하고 정리해보자.수식 타이핑이 너무 힘들어서 중간 중간 결과만 써보면,
$\frac{K_{c}}{(s+1)^{3}}$
\( =\frac{K_{c}}{1-3 \omega^{2}+\omega\left(3-\omega^{2}\right) j} \)
위 식으로부터 위상각 탄젠트 값은,
\( \tan \phi=\frac{\omega\left(\omega^{2}-3\right)}{1-3 \omega^{2}} \)
위상각이 -180˚일때 탄젠트값은 0이므로,
ω^2 = 3 이고, 이 때 ω는 크로스오버 주파수 $\omega_{c o}$ 이다.
진폭비 AR을 구해보면,\( A R = \frac{K_{c}}{\sqrt{\left.(1-3 \omega^{2}\right)^{2}+\omega^{2}\left(3-\omega^{2}\right)^{2}}} \)
$A R_{O L}\left(\omega_{c o}\right) = 0.5$ 이므로,
AR = 0.5 와 ω^2 = 3 을 대입해주면, Kc = 4
----------------------------------------------------------------------------------------------------
68. 교반탱크에 100L의 물이 들어있고 여기에 10%의 소금용액이 5L/min로 공급되며 혼합액이 같은 유속으로 배출될 때 이 탱크의 소금농도식의 Laplace 변환은?
① $Y(s)=0.05\left(\frac{1}{s}-\frac{1}{s+0.05}\right)$
② $Y(s)=0.05\left(\frac{1}{s}-\frac{1}{s+0.1}\right)$
③ $Y(s)=0.1\left(\frac{1}{s}-\frac{1}{s+0.05}\right)$
④ $Y(s)=0.1\left(\frac{1}{s}-\frac{1}{s+0.1}\right)$
정답 : 3번
----------------------------------------------------------------------------------------------------
15년 4회 41번하고 개념은 비슷하다. 이 문제가 식을 세우거나 계산이 좀더 복잡하다.
https://for-freeedom.tistory.com/212
화공기사 2015년 4회 기출 풀이(41번,42번,43번,44번,45번)
* 합격을 위해 맞춰야할 문제 : 41번, 42번, 43번, 44번 41. 바닥면적 4㎡ 의 빈 수직탱크에 물이 f(t) = 10L/min 의 유속으로 공급될 때 시간에 따른 탱크 내부의 액위(m) 변화 h(t)와 라플라스 변환된 H(s)는
for-freeedom.tistory.com
약간의 반응공학 등에서 공부한 개념을 사용하여 식을 세워보면,
V * dC/dt = Q * C_in - Q * C
100L * dC/dt = 5 L/min * 0.1 - 5 L/min * C
100 * dC/dt = 0.5 - 5C
여기까지 하고, 이 문제에서는 C가 아니라 y 이므로 y로 써보면,
100 * dy/dt = 0.5 - 5y
라플라스 변환하면,
100sY(s) = 0.5/s - 5Y(s)
Y(s)로 정리하면,
Y(s) = 0.5 / s(100s+5)보기에 있는 형태로 바꿔보면,Y(s) = 0.1/s - 10/(100s+5)
Y(s) = 0.1/s - 0.1/(s+0.05)
Y(s) = 0.1 * (1/s - 1/(s+0.05)
----------------------------------------------------------------------------------------------------
69. 어떤 1차계의 전달함수는 1/(2s+1)로 주어진다. 크기 1, 지속시간 1인 펄스입력변수가 도입되었을 때 출력은?
(단, 정상상태에서의 입력과 출력은 모두 0이다.)
① $1-t e^{-t / 2} u(t-1)$
② $1-e^{-(t-1) / 2} u(t-1)$
③ $1-\left\{e^{-t / 2}+e^{-(t-1) / 2}\right\} u(t-1)$
④ $1-e^{-t / 2}-\left\{1-e^{-(t-1) / 2}\right\} u(t-1)$
정답 : 4번
----------------------------------------------------------------------------------------------------
전달함수는 1/(2s+1)로 주어져있고, 크기1인 입력변수는 step function으로
step function 의 라플라스 변환은 1/s 이다.
그래서 1/s * 1/(2s+1) 의 라플라스 역변환을 구하면 되는데
문제는 여기서 step function의 지속시간이 1이다.
이럴때는 주어진 전달함수를 1초 시간지연시켜서 빼주면 된다.
a 만큼 시간지연이 있을 때 e^-as 를 곱해주면 되는데
여기서 a=1이고, 1/s * 1/(2s+1) * e^-s 를 빼주면 된다.
정리하면,
Y(s) = [1/s * 1/(2s+1)] - [1/s * 1/(2s+1) * e^-s]
이 식을 역변환하면 되는데
1/s * 1/(2s+1) 의 라플라스 역변환을 구해보면
1/s * 1/(2s+1) = 1/s - 1/(s+0.5) 에서
역변환은 1 - e^(-0.5t) 이다.
라플라스 테이블에 아래와 같이 시간지연 관련된게 있는데
$f(t-a) u(t-a)$ ↔ $\mathcal{L}(x)=e^{-a s} \mathcal{L}(f(t))$
1/s * 1/(2s+1) * e^-s 이 식을 역변환하는데 그대로 적용하면,
역변환은 {1 - e^(-0.5(t-1))} * u(t-1) 이 된다.
결론은,
Y(s) = [1/s * 1/(2s+1)] - [1/s * 1/(2s+1) * e^-s] 식을 역변환하면,
1 - e^(-0.5t) - {1 - e^(-0.5(t-1))} * u(t-1)
----------------------------------------------------------------------------------------------------
70. 다음 함수의 Laplace 변환은?
(단, u(t)는 단위계단함수이다.)
f(t)=h{u(t-A)-u(t-B)}
① $F(s)=\frac{h}{s}\left(e^{-A s}-e^{-B s}\right)$
② $F(s)=\frac{h}{s}\left\{1-e^{-(B-A) s}\right\}$
③ $F(s)=\frac{h}{s}\left\{1-e^{(B-A) s}\right\}$
④ $F(s)=\frac{h}{s}\left(e^{-A s}-e^{B s}\right)$
정답 : 1번
----------------------------------------------------------------------------------------------------
위 69번 문제에서 개념은 다 나왔다.
단위계단함수의 라플라스 변환은 1/s 이고,
시간지연이 A만큼 있을 때 e^-As 를 곱해주면 된다.
----------------------------------------------------------------------------------------------------
'화공기사 > 2022년 1회 필기 기출 풀이' 카테고리의 다른 글
| 화공기사 2022년 1회 기출 풀이(76번,77번,78번,79번,80번) (2) | 2022.03.31 |
|---|---|
| 화공기사 2022년 1회 기출 풀이(71번,72번,73번,74번,75번) (0) | 2022.03.31 |
| 화공기사 2022년 1회 기출 풀이(61번,62번,63번,64번,65번) (0) | 2022.03.29 |
| 화공기사 2022년 1회 기출 풀이(56번,57번,58번,59번,60번) (0) | 2022.03.28 |
| 화공기사 2022년 1회 기출 풀이(51번,52번,53번,54번,55번) (0) | 2022.03.28 |




댓글