* 76번~80번
76. 수송 지연(transportation lag)의 전달함수가 $G(s)=e^{-\tau_{a} s}$일 때, 위상각(phase angle; $\phi$)은?
(단, ω는 각속도를 의미한다.)
① $\phi=-\omega \tau_{a}$
② $\phi=\frac{1}{\omega \tau_{a}}$
③ $\phi=\frac{1}{1+\omega \tau_{a}}$
④ $\phi=\frac{1}{\sqrt{1+\omega \tau_{a}}}$
정답 : 1번
----------------------------------------------------------------------------------------------------
시간지연 항의 위상각은
$\phi=-\omega \tau_{a}$ 이다.
16년 1회 53번 같은 문제를 풀 때 기본적인 내용이 된다.
https://for-freeedom.tistory.com/196
화공기사 2016년 1회 기출 풀이(51번,52번,53번,54번,55번)
* 합격을 위해 맞춰야할 문제 : 54번, 55번 51. 변수 값을 측정하는 감지시스템은 일반적으로 센서, 전송기로 구성된다. 다음 중 전송기에서 일어나는 문제점으로 가장 거리가 먼 것은? ① 과도한
for-freeedom.tistory.com
----------------------------------------------------------------------------------------------------
77. $\frac{Y(s)}{U(s)}=\frac{1}{s^{2}+5 s+6}$의 전달함수를 갖는 계에서 $y_{1}=y, y_{2}=\frac{d y}{d t}$라고 할 때, 상태함수를 $\left[\begin{array}{c} \dot{y_{1}} \\ \dot{y_{2}}\end{array}\right]=A\left[\begin{array}{l}y_{1} \\ y_{2}\end{array}\right]+B u$로 나타낼 수 있다. 이 때, 행렬 A와 B는?
(단, 문자 위 점 " ˙ "은 시간에 대한 미분을 의미한다.)
① $A=\left[\begin{array}{rr}0 & 1 \\ -2 & -3\end{array}\right], \quad B=\left[\begin{array}{l}1 \\ 1\end{array}\right]$
② $A=\left[\begin{array}{rr}0 & 1 \\ 2 & 3\end{array}\right], \quad B=\left[\begin{array}{l}0 \\ 1\end{array}\right]$
③ $A=\left[\begin{array}{rr}0 & 1 \\ -6 & -5\end{array}\right], \quad B=\left[\begin{array}{l}0 \\ 1\end{array}\right]$
④ $A=\left[\begin{array}{rr}0 & 1 \\ -5 & -6\end{array}\right], \quad B=\left[\begin{array}{l}1 \\ 0\end{array}\right]$
정답 : 3번
----------------------------------------------------------------------------------------------------
거의 뭐 행렬 제대로 계산해본지 10년도 넘은거 같은데..
잘 모르겠어서 구글링하다보니 이런걸 찾았다.
전달함수를 상태방정식으로 변환하는 방법이다.
각 변수의 관계가 1차 미분 관계로 정의되는 경우를 위상변수라고 하는데,
$\begin{aligned} \frac{d^{n} y}{d t^{n}} &+a_{n-1} \frac{d^{n-1} y}{d t^{n-1}}+\cdots+a_{1} \frac{d y}{d t}+a_{0} y=b_{0} u \\ x_{1} &=y \\ x_{2} &=\frac{d y}{d t}=\dot{x}_{1} \\ x_{3} &=\frac{d y^{2}}{d t^{2}}=\dot{x}_{2} \\ & \vdots \\ x_{n} &=\frac{d y^{n-1}}{d t^{n-1}}=\dot{x}_{n-1} \\ \frac{d y^{n}}{d t^{n}} &=\dot{x}_{n}=-a_{0} x_{1}-a_{1} x_{2} \cdots-a_{n-1} x_{n}+b_{0} u \end{aligned}$
이러한 미분방정식으로 표현될 때, 아래와 같이 상태방정식을 쓸 수 있다.
$\left[\begin{array}{c}\dot{x}_{1} \\ \dot{x}_{2} \\ \dot{x}_{3} \\ \cdot \\ \cdot \\ \cdot \\ \dot{x}_{n-1} \\ \dot{x}_{n}\end{array}\right]=\left[\begin{array}{cccccccc}0 & 1 & 0 & 0 & . & . & . & 0 \\ 0 & 0 & 1 & 0 & . & . & . & 0 \\ 0 & 0 & 0 & 1 & . & . & . & 0 \\ . & . & . & . & . & & \\ . & . & . & . & & . & & . \\ . & . & . & . & & . & . \\ 0 & 0 & 0 & 0 & . & . & . & 1 \\ -a_{0} & -a_{1} & -a_{2} & -a_{3} & . & . & . & -a_{n-1}\end{array}\right]\left[\begin{array}{c}x_{1} \\ x_{2} \\ x_{3} \\ . \\ \cdot \\ \cdot \\ x_{n-1} \\ x_{n}\end{array}\right]+\left[\begin{array}{c}0 \\ 0 \\ 0 \\ . \\ . \\ \cdot \\ 0 \\ b_{0}\end{array}\right] u$
뭐 어차피 문제에서 주어진 건 2by2 행렬이니,
사이즈 줄여서 다시써보면,
\( \frac{d^{2} y}{d t^{2}}+a_{1} \frac{d y}{d t}+a_{0} y=b_{0} u \)
\( \left\{\begin{array}{l}y_{1}=y \\ y_{2}=\dot{y}=\dot{y}_{1}\end{array}\right. \)
일 때,
\( \left[\begin{array}{l}\dot{y}_{1} \\ \dot{y}_{2}\end{array}\right]=\left[\begin{array}{cc}0 & 1 \\ -a_{0} & -a_{1}\end{array}\right]\left[\begin{array}{l}y_{1} \\ y_{2}\end{array}\right]+\left[\begin{array}{l}0 \\ b_{0}\end{array}\right] u \)
여기까지하고, 문제에서 주어진 전달함수를 정리해보자
\( \left(s^{2}+5s+6\right) Y(s)=U(s) \)
초기조건을 0이라 가정하고 Laplace 역변환하면,
\( \frac{d^{2} y}{d t^{2}}+5 \frac{d y}{d t}+6 y=u \)
위에서 썼던 식하고 비교해보면, a0=6, a1=5, b0=1 이다.
이제 또 위에서 썼던 2by2 행렬에 그대로 대입해주면,
$A=\left[\begin{array}{rr}0 & 1 \\ -6 & -5\end{array}\right], \quad B=\left[\begin{array}{l}0 \\ 1\end{array}\right]$
을 확인할 수 있다.
----------------------------------------------------------------------------------------------------
78. $F(s)=\frac{5}{s^{2}+3}$의 라플라스 역변환은?
① $f(t)=5 \sin \sqrt{3} t$
② $f(t)=\frac{5}{\sqrt{3}} \cos 3 t$
③ $f(t)=5 \cos \sqrt{3} t$
④ $f(t)=\frac{5}{\sqrt{3}} \sin \sqrt{3} t$
정답 : 4번
----------------------------------------------------------------------------------------------------
라플라스 테이블 보면된다.
sin ktu(t) ↔ k/(s^2+k^2)
에서 k = 루트3 인 경우이다.
----------------------------------------------------------------------------------------------------
79. 배관계장도(P&ID)에서 공기 신호(pneumatic signal)와 유압 신호(hydraulic signal)를 나타내는 선이 순서대로 옳게 나열된 것은?
①

②
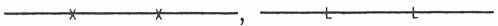
③
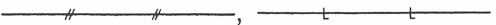
④

정답 : 3번
----------------------------------------------------------------------------------------------------
구글에서 P&ID 레전드 찾아보면 나온다.
보통 도면 첫장에 레전드 보면 다 나와있긴 하다.
----------------------------------------------------------------------------------------------------
80. 공장에서 배출되는 이산화탄소를 아민류로 포집하는 시설을 공정설계 시뮬레이터를 사용하여 모사한다고 할 때 적합한 열역학적 물성 모델은?
① UNIFAC
② Ion - NRTL
③ Peng-Robinson
④ Ideal gas law
정답 : 2번
----------------------------------------------------------------------------------------------------
공정모사 자세히 배우면 이런거 배우는 것 같기도 한데
잘 모르겠다.
----------------------------------------------------------------------------------------------------
'화공기사 > 2022년 1회 필기 기출 풀이' 카테고리의 다른 글
| 화공기사 2022년 1회 기출 풀이(71번,72번,73번,74번,75번) (0) | 2022.03.31 |
|---|---|
| 화공기사 2022년 1회 기출 풀이(66번,67번,68번,69번,70번) (1) | 2022.03.30 |
| 화공기사 2022년 1회 기출 풀이(61번,62번,63번,64번,65번) (0) | 2022.03.29 |
| 화공기사 2022년 1회 기출 풀이(56번,57번,58번,59번,60번) (0) | 2022.03.28 |
| 화공기사 2022년 1회 기출 풀이(51번,52번,53번,54번,55번) (0) | 2022.03.28 |




댓글